Fermat foi um advogado e
matemático francês.Funcionário público, em 1652 foi promovido a Juiz Supremo na Corte Criminal Soberana do Parlamento de Toulouse.
Denominado o 'Príncipe dos amadores', Fermat se ocupava da Matemática apenas como lazer.
Apesar disso, foi considerado um dos maiores matemáticos franceses do século, juntamente com Descartes.
Fluente em línguas tais como italiano, espanhol, basco, latim e grego clássico, Fermat seguiu o costume de sua época de compor restaurações conjecturais de textos sobreviventes à destruição da Biblioteca de Alexandria, já mencionada na aula História da Epistemologia.
Um deles teria
sido o De Locis Planis
(Lugares geométricos das curvas planas)
de Apolônio de Pérgamo,
em que este quase
cria a geometria analítica. Infelizmente, o resultado deste trabalho, embora circulasse em forma de manuscrito desde 1636, só foi publicado póstumamente como Ad Locos Planos et Solidos Isagoge (Introdução aos lugares geométricos de curvas planas e sólidas), em 1679, 43 anos após a publicação de La Géometrie de Descartes, em que este descreve, num contexto filosófico e não matemático, o sistema de eixos, hoje conhecidos como o sistema de coordenadas cartesiano (de Cartesius, forma latina de seu nome, derivada de sua famíla ser fabricante de mapas e cartas náuticas), como vimos na aula As Contribuições de Galileu e Newton. Por mérito, deveriam, talvez, ser chamadas de 'coordenadas Fermatianas'.
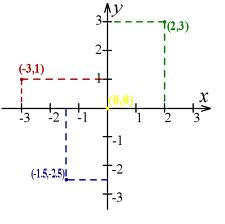
Essa construção levou à Geometria Analítica.
Afável, mas
reservado,
divulgava suas descobertas por
correspondência com o padre matemático Mersenne,
que, na ausência de periódicos
científicos,
tornou-se ele mesmo um centro
de divulgação, mantendo e repassando
correspondência com os
maiores cientistas da época, tais como Descartes, Galileu, Pascal
e Torricelli,
o que, afinal, às vezes causava disputas de
precedência nas descobertas.Dessa troca de correspondências, acabou envolvido em ácidas polêmicas com o melindroso Descartes. Uma vez, Descartes o desafiou para encontrar a tangente à curva, hoje conhecida como folium de Descartes,
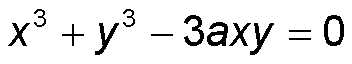
cujo gráfico é (para a=1)
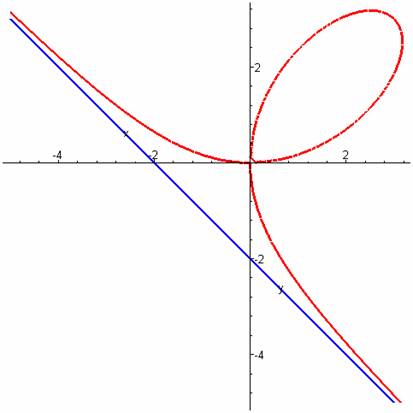
um problema que o próprio Descartes não sabia resolver e, por isso, tinha certeza que Fermat não conseguiria também. Para seu desespero, Fermat facilmente encontrou a tangente, graças a um método para determinação de máximos, mínimos e tangentes às diversas curvas, que ele desenvolveu a partir de suas pesquisas com lugares geométricos, e que era equivalente a diferenciação.
Na verdade, Newton declarou que suas próprias idéias iniciais sobre o cálculo vieram diretamente da "maneira de Fermat de traçar tangentes".
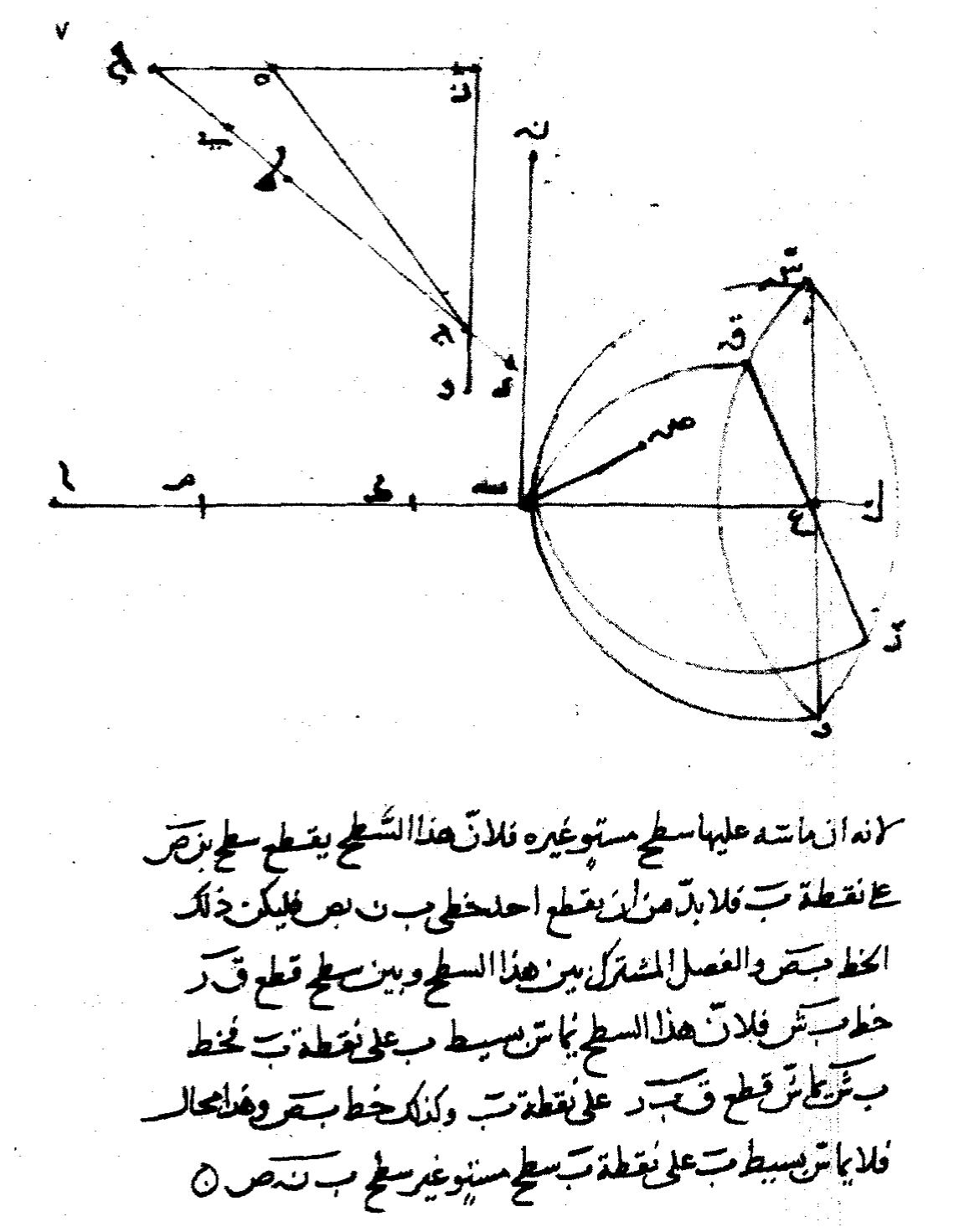
Em 1657, Fermat demonstrou a Lei da Refração que fornece o desvio angular sofrido por um raio de luz ao passar de um meio para outro com índice de refração diferente:
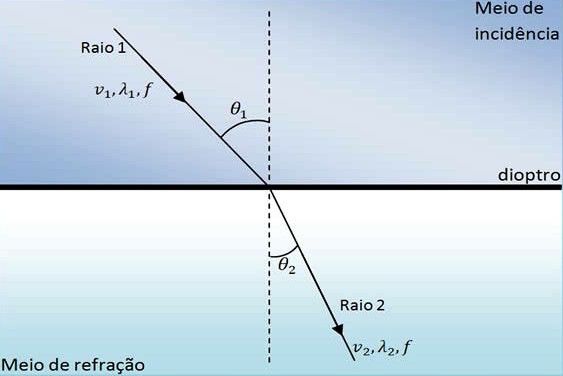
Ibn Sahl, matemático, físico e ótico persa, já havia derivado essa lei em seu livro Sobre espelhos e lentes incendiários, publicado em 984.
Snell, astrônomo e
matemático
holandês redescobriu essa lei em 1621 mas nunca a publicou.
Descartes
incluiu uma derivação dessa lei em seu Discours
de la
méthode, em 1637, usando argumentos
heurísticos de conservação de
momentum, havendo quem sustente que ele
'cozinhou' essa derivação a partir do trabalho de
Snell. Por
esse motivo, na França, essa lei é conhecida como
Lei de
Descartes, em outros países como Lei de
Snell,
enquanto no Brasil, referimos a Lei de Snell-Descartes.Fermat rejeitou a derivação de Descartes e chegou à mesma fórmula baseando-se apenas no seu Princípio do Menor Tempo, que generalizava o Princípio de Menor Percurso de Herão de Alexandria (60 d.C.), e foi transformado no Princípio da Mínima Ação, na Mecânica, em 1744, por Maupertuis, conforme veremos na próxima aula. Considera-se que aquele foi o primeiro princípio variacional enunciado na Física desde o princípio de Herão.
Segundo esse princípio, a trajetória seguida por um raio luminoso de um ponto A para um ponto B é tal que o tempo decorrido nesse percurso é mínimo. Isto quer dizer que, dentre todos os caminhos possíveis do ponto A ao ponto B, a Natureza 'escolhe' aquele em que o tempo decorrido é o menor deles.
A figura abaixo demostra como, no caso de uma reflexão, o caminho no qual o ângulo de reflexão é igual ao de incidência, 'escolhido' pela Natureza, é justamente aquele minimiza o percurso.
Fermat manteve também correspondência com Pascal (vide adiante), que lhe propôs problemas sobre jogos de azar, o que levou a que, juntos, determinassem as regras essenciais da probabilidade e lançassem os fundamentos da Teoria da Probabilidade.
No entanto, Fermat tratava essas questões apenas como desafios a serem resolvidos, tendo sempre a Teoria dos Números como foco de interesse, como veremos a seguir.
Inspirado
pela
leitura de uma tradução latina, de 1621, da Aritmetica
de Diofanto
de Alexandria, Fermat enveredou num estudo da Teoria dos Números,
especialmente
sobre os números primos.Dentre os vários teoremas que descobriu, o assim chamado Último Teorema de Fermat, inspirado nas equações diofantinas, é, certamente, o mais famoso.
De fato, é uma extensão a potências mais altas do bem conhecido Teorema de Pitágoras
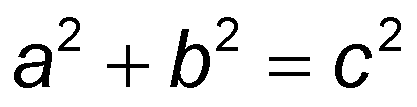
Seu enunciado é
Não há solução com x, y, z inteiros positivos e n inteiro, n>2 para
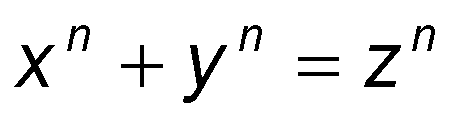
Segundo a lenda, escreveu, ao lado do enunciado desse problema, às margens de seu exemplar de Aritmetica, como era seu costume:
"Encontrei uma demonstração verdadeiramente maravilhosa disto, mas esta margem é estreita demais para contê-la."
Fermat, em geral, não deixou provas de seus vários teoremas, alguns dos quais, só foram provados muito tempo depois. O pequeno teorema de Fermat, por exemplo, só foi demonstrado por Euler em 1736. Outras conjeturas, tais como a de que "todos os números na forma hoje conhecida como números de Fermat são primos", provaram ser falsas.
Aquela nota sugeria haver uma demonstração elementar do teorema e, portanto, desde então, praticamente todos os grandes expoentes da Matemática (incluindo os grandes Euler e Gauss), pelos três séculos seguintes, tentaram demonstrar ou desprovar esse teorema, sendo ele, por isso, até incluído no Livro Guinness dos Recordes, como o problema mais difícil de Matemática.
Em 1906, Paul Wolfskehl, um industrial apreciador de matemática, constituiu um prêmio de 100.000 marcos alemães para quem o demonstrasse.
Além de milhares de amadores com pretensas provas de nível escolar, muitos matemáticos ao longo do tempo conseguiram provas parciais, para expoentes específicos.
Dois casos particulares interessantes são
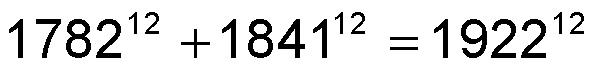
e
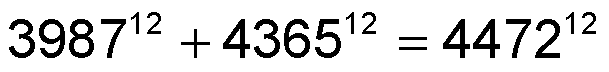
O Último Teorema de Pitágoras entrou para a cultura popular e já foi mencionado em inúmeras obras literárias, filmes, canções, etc.
Naturalmente, com o aparecimento dos computadores, milhares de expoentes foram testados. Em 1994 o teorema já tinha sido verificado para todos os expoentes abaixo de quatro milhões. Mas isso, é claro, ainda não era a prova desejada.
Só foi demonstrado em 1995, por Andrew Wiles, não com uma "demonstração verdadeiramente maravilhosa" e simples, como Fermat alegava possuir, mas envolvendo ferramentas matemáticas indisponíveis à época, tais como curvas elípticas, formas modulares e representações galoisianas. Por isso, acredita-se que, na verdade, ou Fermat não tinha nenhuma demonstração ou, se a tinha, não era correta.
Além do prestígio, Wiles recebeu, também, o prêmio instituído por Wolfskehl, embora bastante reduzido, devido à hiperinflação alemã da 2a. Guerra Mundial.
Como um bônus, várias ferramentas e técnicas matemáticas foram desenvolvidas, como subproduto desse esforço multissecular pela demonstração.
Veja, também, esta página:
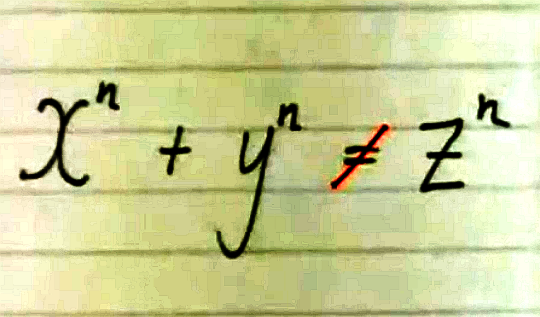vídeos
sobre o Último Teorema de Fermat
Continue
conhecendo a Revolução na Matemática.Voltar à Parte Anterior
Voltar a Minhas Aulas.
Voltar ao começo desta página
Voltar à página principal de Física Interessante
