Para compreender melhor as contribuições de Galileu e Newton, é preciso retornarmos ao pensamento anterior vigente que, como vimos na aula História da Epistemologia, era basicamente o de Aristóteles, o qual prevaleceu na Europa durante toda a Idade Média.
Vale a pena lembrar que, embora Aristóteles tenha escrito um livro intitulado Física, este é, na verdade, uma coleção de estudos filosóficos sobre a Natureza, tanto sobre os seres vivos como sobre os inanimados.
Ademais,
na 'física' aristótelica,
'movimento'
era um conceito mais vasto, metafísico,
que englobava
qualquer tipo de mudança, não
só de posição, incluindo as
noções de 'crescimento', 'alteração'
e 'mudança'. No Física, Aristóteles investiga os princípios e as 'causas' das coisas e das 'mudanças'.
Segundo ele, há quatro causas:
Em seu livro Fédon, Platão afirmava que a verdadeira explicação de qualquer fenômeno físico deve ser teleológica (estudo das finalidades, não confundir com Teologia - o estudo sobre a divindade). Enfatizando a distinção entre as causas necessárias (causa material) e causas suficientes (causa teleológica) das coisas, ele dizia que o movimento e a ação dos corpos dependem destas últimas, as quais seriam determinados pelas finalidades impostas a eles pelo Demiurgo (Deus-artesão).
Note-se que esta ideia é compatível com a noção de que
não cai uma folha da árvore se não for a Vontade de Deus,
que, na verdade, não está na Bíblia, como muitos pensam, mas assemelha-se a
não cai uma folha (da árvore) sem que Ele disso tenha ciência
que se encontra na 6ª Surata, versículo 59, do Alcorão.
Aristóteles desenvolveu, então, a ideia de causa final que ele acreditava que era explicação determinante de todos os fenômenos, ou seja, além das causas materiais, necessárias para o fenômeno, a finalidade desse fenômeno, imposta externamente, é que iria determinar se ele iria realmente acontecer ou não.
Note-se que essa causa final, teleológica, por vezes, sugere um propósito e uma intencionalidade nos fenômenos, como se a flecha 'quisesse' atingir o alvo e a semente 'quisesse' tornar-se uma árvore.
Uma
estátua:
Pedra em
movimento:
Para Aristóteles, o movimento é impossível no vazio, pois falta um referencial com relação ao qual se determina o movimento.
Aristóteles estava bem consciente de que, no vazio (vácuo), sem a resistência do ar, todos os corpos, 'leves' e 'pesados' cairiam à mesma velocidade, o que para Aristóteles era absurdo; 'portanto' ele concluiu que o vácuo não pode existir (!)
Para ele, o movimento é sempre visto como um efeito, resultado de uma causa, a força:
Nullum violentum potest esse perpetuum (o movimento forçado não pode manter-se sozinho) (Aristótles, De Caelo, apud Dugas, 1955, p. 21)
Isto quer dizer que, para Aristóteles, cessada a força (causa), cessa o movimento (efeito).
Com isso, o equivalente à 2ª Lei de Newton
F = m•a,
onde
F = p•v,
onde
De acordo com a 4ª causa aristotélica, vista acima, o ponto de destino do movimento era considerado o lugar natural daquele objeto.
Com isso, haveria dois tipos de movimento:
Por outro lado, haveria dois tipos de corpos:
Para explicar essa noção de 'lugar natural', Aristóteles utilizou a teoria dos quatro elementos: terra, água, ar e fogo. Segundo ela, todas as coisas seriam compostas de misturas desses quatro elementos.
Ora, esses elementos teriam gaus diferentes de 'gravidade':
a terra
afunda na água,
o ar
flutua na água
o fogo
flutua no arAssim, se poderia estabelecer a seguinte hierarquia:
| símbolo | elemento |
 |
Fogo |
 |
Ar |
 |
Água |
 |
Terra |
Os dois primeiros, tendendo para cima, teriam no céu o seu lugar natural, enquanto que os dois últimos teriam lugar natural no chão, como, aliás, indicam seus símbolos tradicionais.
Com isso, conforme o elemento que predominasse na mistura, a substância seria mais 'leve' ou menos 'pesada'.
Por exemplo,
uma pedra
seria uma mistura com predomínio da terra
e seria,
portanto, pesada ('grave') e seu
lugar natural seria o chão
as nuvens
seriam formadas por
uma mistura de água e ar em que
predomina o último,
fazendo com que
fossem imponderáveis e flutuassem no ar,
tendo o céu
como lugar
natural.Assim, por exemplo, numa sociedade estratificada como a grega,
um filho de
escravos teria seu lugar
natural na base da pirâmide social e, com isso,
não podia almejar
qualquer ascensão social, pois isso seria contra
natura (antinatural, contra as 'leis da natureza')
uma mulher,
também em
posição inferior na escala grega, teria seu lugar
natural na casa, na
procriação e educação dos
filhos; uma mulher que conseguisse uma
influência maior seria uma 'desnaturada',
por
exemplo, uma prostituta ou uma bruxa
um nobre,
com lugar natural no topo da
escala social, não poderia nunca 'cair' dela; de fato, nas
lendas e
narrativas, muitas vezes o 'herói' é feito
escravo, mas sempre o
destino se encarrega de fazer o seu 'valor' ser reconhecido,
conquistar os favores de seu amo e, portanto, recolocá-lo no
seu lugar
natural. Veja-se, por exemplo, a história bíblica
de José que foi feito
escravo e,
depois, se tornou chanceler do Egito.
Embora essa
teoria
explicasse razoavelmente bem
a queda e o
movimento vertical dos corpos, já na época de
Aristóteles, todavia,
questionava-se, por exemplo, o que manteria uma flecha em
movimento
após deixar o arco que a pos em movimento? Para
responder
essa
pergunta, Aristóteles utilizou a idéia de antiperistasis.
Segundo ela,
Todavia, embora descrevessem bem os fenômenos no mundo sublunar (terrestres), formado por corpos sujeitos a geração e corrupção (criáveis e deterioráveis), a matéria celeste é constituída por um éter inextinguível e incorruptível.
O chamado Islamismo floresceu no século VII na Península Arábica, a qual integrava territórios onde a ciência já se tinha desenvolvido, tais como o Egito sob os Ptolomeus e a Pérsia dos sassânidas.
Seu livro sagrado, o Corão, valorizava a Ciência, considerava que a Medicina era uma arte próxima de Deus.
Inicialmente, era uma comunidade fértil, com uma grande variedade de povos e raças muito tolerante com estrangeiros e novas idéias.
Vários manuscritos gregos e de outras partes do mundo, especialmente os de Platão e de Aristóteles, foram traduzidos para o árabe e, nos finais do século IX, já tinham sido assimilados pela civilização islâmica.
No entanto, em vez do Escolasticismo paralizante da Europa, a ciência árabe avançou:
Dentre seus vários pensadores, vale destacar
Mais conhecido no Ocidente como Al-Biruni, era viajante, tolerante e eclético e deixou uma monumental obra, com cerca de 150 manuscritos, dedicada a temas de matemática, astronomia e áreas próximas,medicina e farmacologia, metais e pedras preciosas, religião, filosofia, história da Índia.
Conhecido no Ocidente como Alhazen, foi um dos maiores físicos de todos os tempos. Escreveu sobre Matemática, Medicina, Fisiologia, Psicologia e percepção visual.
Introduziu os modelos de partícula para a luz e de intromissão da visão: vemos porque a luz refletida pelo objeto entra no nosso olho.
Precedendo Bacon e Galileu, defendeu a abordagem quantitativa e empírica da ciência.
Formulou o que se tornaria, muito depois, conhecido como o Princípio da Mínima Ação, proposto por Maupertuis, em 1744 (conforme veremos na aula A Revolução na Matemática - Parte 2).
Sobre ele, o físico Abdus Salam, ganhador do Prêmio Nobel, escreveu:
Ibn al-Haytham foi um dos maiores físicos de todos os tempos. Ele fez contribuições experimentais de níveis mais altos na óptica. Ele enunciou que um raio de luz, ao passar por um meio, segue o caminho que é mais fácil e "mais rápido". Aqui ele estava antecipando por vários séculos o princípio de Fermat do trajeto mínimo da luz. Ele enunciou a lei da inércia, que viria a ser mais tarde a primeira lei de Newton. A parte V de "Opus Majus", de Roger Bacon, é praticamente uma explicação da Óptica de Alhazen. (Islam and Science. In: C. H. Lai. Ideals and Realities: Selected Essays of Abdus Salam. 2nd ed.. Singapore: World Scientific, 1987, p. 179-213)
Durante a
alta Idade
Média, várias igrejas católicas davam
aulas no
próprio salão da igreja que eram destinadas aos
filhos de
nobres que pretendiam seguir a carreira religiosa. Aos poucos, as
escolas ganharam salas adjacentes e novos edifícios. No
século 12, deram origem às universidades.
(NARLOCH, 2013,
p. 55). Criadas e dirigidas por padres, começaram a surgir as primeiras universidades na Europa:
Compare-se com a nossa mais antiga: Paraná (1912). Aliás, segundo Olive,
"a criação da Universidade do Rio de Janeiro, ocorrida em 1920 por iniciativa do Governo Federal, ocorreu devido à visita que o Rei da Bélgica faria ao país, em virtude das comemorações ao Centenário da Independência do Brasil. Com isso, o governo brasileiro pretendia conceder o título Doutor Honoris Causa, porém o país carecia de uma instituição propriamente universitária." (OLIVE, 2002)
No entanto, compare-se, também, com as, frequentemente esquecidas, mais antigas do mundo:
As universidades européias foam organizadas segundo o esquema de três conteúdos iniciais (o Trívio):
seguidos pelo Quadrívio:
Apesar disso, embora a Teologia fosse o curso com maior
status,
"exigia-se dos filósofos naturais das faculdades que se
abstivessem de introduzir Teologia e temas de fé na
filosofia
natural" (GRANT, apud NARLOCH, 2013, p. 55).
Conforme vimos na aula Racionalismo e Empirismo, a Escolástica era o método de ensino prevalecente nas universidades europeias durante a Idade Média, com forte ênfase na dialética e na inferência, dogmático, embasado na Bíblia e nas obras de Aristóteles e de Platão como as únicas fontes de conhecimento.
No
método escolástico
debatiam-se questões e opiniões,
fundamentando-as com a razão e a retórica, sem
uso da Matemática. Ficou famosa a
questão "Quantos
anjos podem dançar na cabeça de um alfinete?"
e suas
variantes, tal como aparece na Summa Theologica
(ca. 1270) de Tomás de Aquino. Com o avanço do capitalismo urbano, houve a necessidade de pessoas habilitadas para a função pública, o que contribuiu para a ascensão do Humanismo renascentista, com sua veneração à Antiguidade Clássica, expandindo-se de Florença para toda a Europa, entre os séculos XIV e XVI, com sua valorização
Com o desenvolvimento do capitalismo, muitos burgueses enriqueceram e tornaram-se mecenas, patrocinando artistas, literatos e atividades artísticas e culturais em geral. Segundo Roque (2012),
"Os humanistas eram, em sua maioria, autodidatas que trabalhavam fora das universidades, sob o regime de mecenato, e por isso, não aderiram ao espírito escolástico. [...] Muitos humanistas eram matemáticos da corte e alternavam suas atividades de ensino, ou literárias, com funções políticas" (ROQUE, 2012, p. 296).
Joannes Philoponus (do grego Philoponus, amante da labuta), também conhecido como João, o Gramático, foi um filósofo cristão e neoplatônico grego nascido na Alexandria, norte do Egito. Foi, talvez, o primeiro a rejeitar idéias básicas de Aristóteles. Escreveu cerca de 40 livros sobre Teologia e Filosofia.
Rejeitou a antiperistasis e o motor interno de Aristóteles, propondo, em seu lugar, a ideia do impetus, propriedade semelhante ao 'impulso', infusa no objeto quando do seu lançamento e responsável pela continuação de seu movimento, comparável ao calor que se infunde e acompanha um objeto que tocou uma fonte de calor.
No entanto, sua crítica a Aristóteles foi tão radical que foi negligenciada pelos Escolásticos e ignorada por séculos até o século XIV, quando Buridan as retomou e desenvolveu.
Buridan
foi um sacerdote francês.O impetus pode ser entendido como a mpressão de um poder de auto-movimento.
Como
vimos na aula Realismo e Empirismo, Copérnico
superou a mera acumulação
de dados
astronômicos e ajustes no
modelo Ptolomaico e propos um novo modelo, heliocêntrico,
uma
explicação mais plausível para as
observações.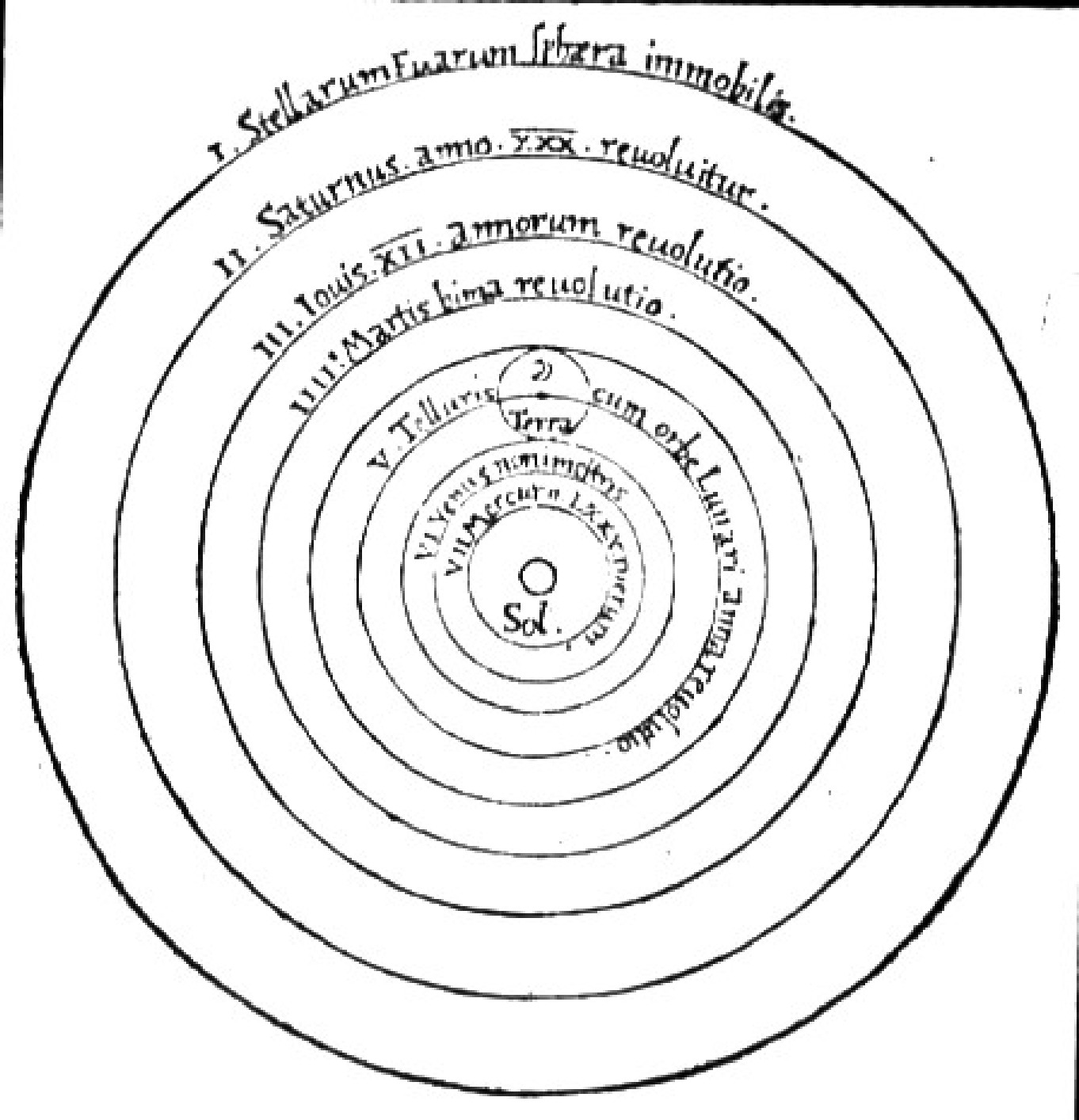
Vimos também que, segundo Roque (2012),
"antes de 1580 quase nenhum astrônomo acreditava que o modelo de Copérnico pudesse representar a estrutura física do cosmos. [...] até os anos 1570, quando as observações realizadas por Tycho Brahe abriram novas possibilidades. Somente por volta de 1600 os astrônomos europeus pareciam estar preparados para aceitar a realidade física do sistema heliocêntrico" (ROQUE, 2012, p. 294-295).
"O Classicismo produziu obras que retratam um universo harmônico, onde as leis matematizáveis da natureza regulam todo o seu funcionamento." (REIS; GUERRA; BRAGA, 2006)
O homem medieval via em Deus a razão de todas as coisas.
Os renascentistas acreditavam no poder humano de julgar, de criar e construir.
O Renascimento caracteriza-se por enormes progressos nas artes, nas leis e nas ciências.
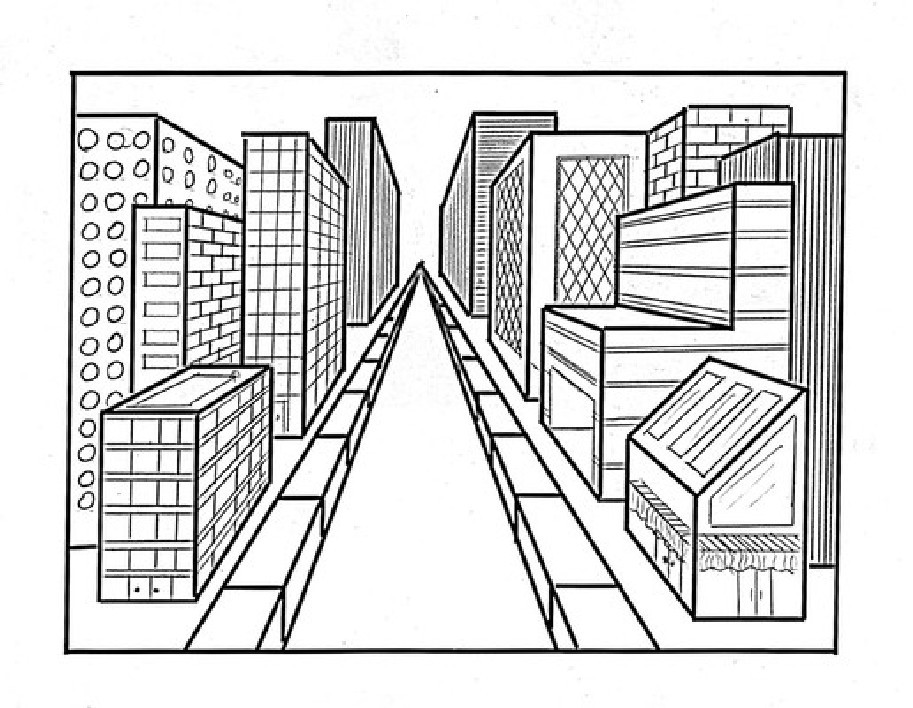
Arquitetura Gótica: catedrais: homem dominado pelo espaço, olhar para cima, em busca de Deus
Arquitetura Renascentista: perspectiva: homem domina o espaço, olhar para a frente, para o futuro brilhante que aguarda o Homem e é construído por ele.
Leonardo
da Vinci foi pintor,
escultor, arquiteto, físico, engenheiro, botânico
e músico do
Renascimento Italiano.Foi considerado um dos maiores gênios da história da Humanidade, embora sem nenhum estudo formal na maioria dessas áreas, com um QI estimado entre 180 e 220.
Leonardo foi aluno e amigo de Luca Pacioli, de quem ilustrou o famoso livro De Divina Proportioni que tratava da proporção ideal, conhecida como Razão Áurea.
Seu Homem vitruviano, baseado na obra de Marcus Vitruvius Pollio, arquiteto e engenheiro romano do séc. I a.C., tornou-se um símbolo da Renascença e, também, um ícone da cultura pop, tendo sido reproduzido de inúmeras formas, desde o euro até em camisetas.
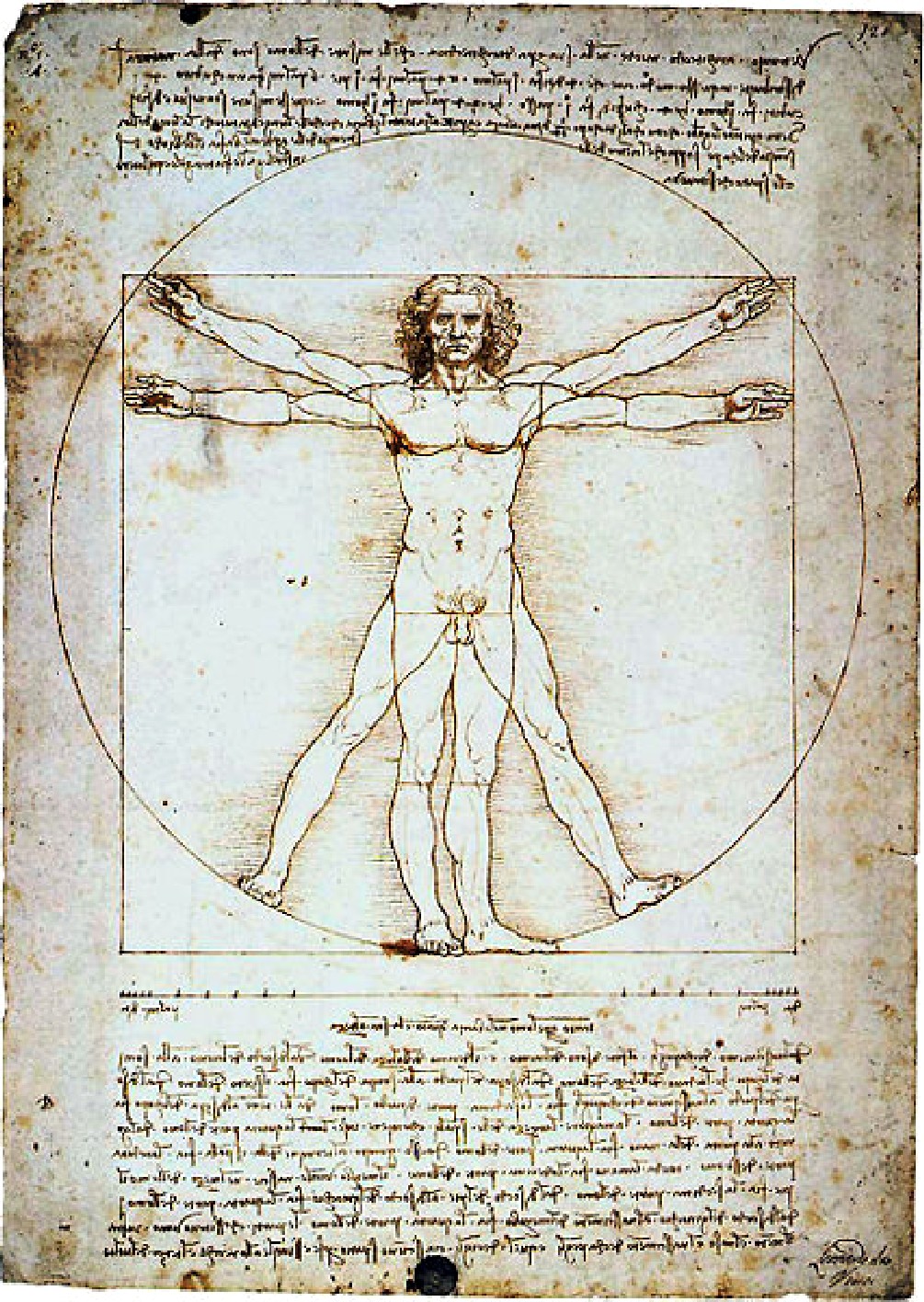
Assim, segundo Vitrúvio, as proporções ideais de um ser humano devem ser:
Leonardo, na verdade, teve poucas obras acabadas, mas dentre as mais famosas do mundo!
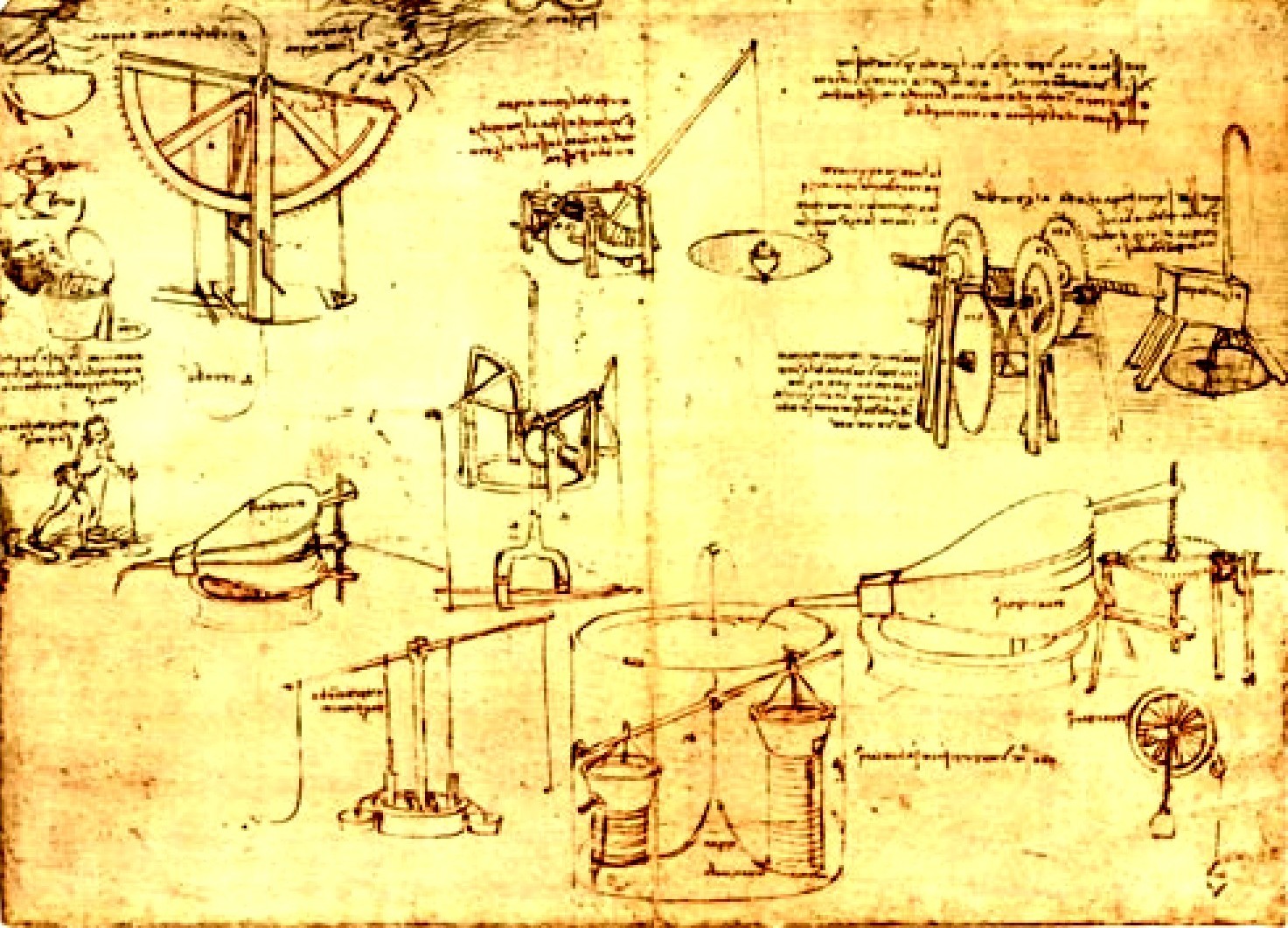
Leonardo deixou cadernos com mais de 13 mil páginas de notas e desenhos fundindo Arte e Ciência, incluindo esboços de
As folhas desses cadernos dispersaram-se em códices em várias bibliotecas e museus do mundo, alguns deles disponíveis online. Dentre eles, o Codex Atlanticus e o O Codex Leicester, o único em mãos privadas, propriedade de Bill Gates, que é exibido apenas uma vez por ano em diferentes cidades do mundo.
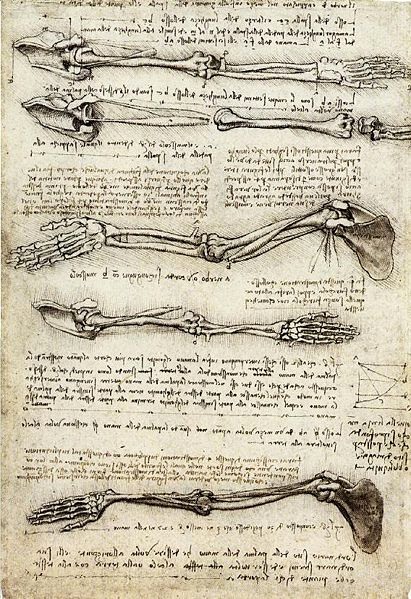
Leonardo participou em autópsias, fez desenhos do esqueleto, músculos, nervos e vasos para produzir melhores pinturas. Geralmente completava suas ilustrações com esboços anatômicos.
Sfumato é uma técnica aperfeiçoada por Leonardo que consiste em sucessivas camadas de cor em gradações sutis, dando a sensação de profundidade, forma e volume. Passou a ser uma técnica universal, um conhecimento básico em pintura.
Chiaroscuro é outra técnica criada por Leonardo, uma forma de perspectiva tonal. O volume tridimensional é sugerido por luzes e sombras fortemente contrastantes. Foi muito usada por Caravaggio, como se verá a seguir.
Perspectiva é uma técnica geométrica de representação da profundidade no plano. Integra cor, luz, forma e espaço. Tendo por base a projeção cônica de Ibn Al-Haitham (mais conhecido pelo seu nome latinizado Alhazen, como vimos na aula História da Epistemologia), foi redescoberta por Brunelleschi, arquiteto e escultor florentino renascentista.
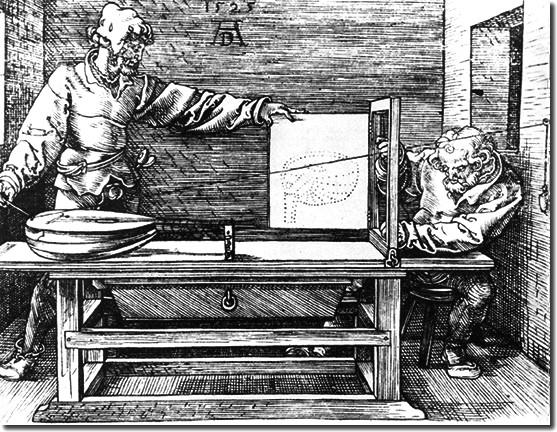
Ela satisfaz o objetivo renascentista de precisão solicitado pelas ciências e substitui a hierarquia simbólica que era representada pelos diferentes tamanhos relativos dos personagens, técnica usada desde os egípcios.
Segundo Edgerton (1995), no entanto, "não há nenhuma naturalidade na representação espacial a partir da perspectiva. De fato, a Perspectiva foi tema de interesse Ocidental, "a utilização desta é fruto da cultura européia ocidental. A Arte Oriental a dispensou até o sec. XIX.
De fato, "os chineses não conseguiam, em um primeiro momento, reproduzir a perspectiva ocidental. Eles não conseguiam ‘ler’ os desenhos ocidentais, pois não trabalhavam com as particularidades da perspectiva geometrizada." (Edgerton, 1995)
Segundo Woortmann (1996), tanto na Ciência como na Arte, ocorreu uma nova concepção de natureza.
"A concepção tradicional era a do propósito: o propósito do Sol é o de gerar luz para os homens, o que explicava sua existência. Contra essa teleologia se manifestaram os pensadores do Renascimento e mais notadamente Galileu, com o novo significado de natureza: um nexo auto-regulado de eventos, obedecendo a suas próprias leis sem qualquer propósito para os humanos. Uma natureza desencantada." (WOORTMANN, 1996)
Para os pioneiros da pintura renascentista, alcançar um maior realismo implicava olhar a natureza, distanciando-se de seus objetos; tomar um "ponto de vista" em sentido literal. A estratégia de Distanzierung - réculer pour mieux sauter [recuar para saltar melhor] - foi comum tanto a cientistas quanto a artistas. (WOORTMANN, 1996)
Segundo Reis, Guerra e Braga (2006),
"é importante salientar que a invenção da perspectiva e do claro-escuro foi extremamente importante, até mesmo crucial, para tornar possíveis as observações empíricas e os registros acurados que fundamentam a ciência moderna." (REIS; GUERRA; BRAGA, 2006)
Segundo Reis, Guerra e Braga (2006), o conhecimento de desenho, especialmente do chiaroscuro, que Galileu adquiriu em Florença, lhe possibilitou compreender a aparência da Lua melhor do que seus antecessores.
Segundo esses autores, a geometrização da projeção das sombras pode lhe ter permitido perceber as irregularidades da superfície lunar, permitindo-lhe, até mesmo, determinar a altura das montanhas lunares, novamente valendo-se da perspectiva.
Com isso,
"a Lua representada por Galileu deixou de ser a imagem da perfeição – associada, no imaginário cristão, à Imaculada Conceição – e passou a ser mais um corpo celeste com características comuns, tal como a Terra. (REIS; GUERRA; BRAGA, 2006)
A pintura de Caravaggio
era dramática, com fundo raso, escuro ou totalmente negro,
com focos
intenso
de luz sobre os detalhes da cena em primeiro plano (rostos, corpos,
etc.).Utilizava uma variante da técnica de chiaroscuro chamada tenebrismo
Madona e Menino Jesus com Serpente
Atendendo a encomenda para decorar a Igreja São Luis dos Franceses, em Roma, esta primeira versão foi contundentemente rejeitada por retratar um São Mateus homem do povo, com pés sujos, segurando com dificuldade a caneta nas mãos pouco habituadas, necessitando do auxílio do anjo. Infelizmente, esta versão foi destruída na Segunda Guerra Mundial.
Esta segunda versão, muito idealizada, foi aceita.
Nesta obra, Caravaggio representou um Cristo atlético, o que chocou seus contemporâneos.
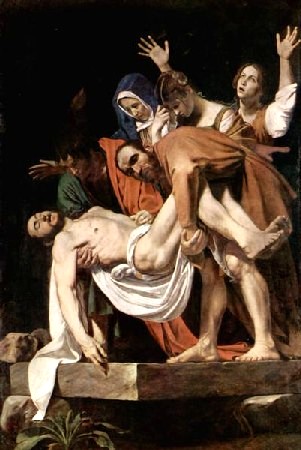
Nesta obra, Caravaggio chocou seus contemporâneos por utilizar uma prostituta que havia morrido afogada como modelo para o rosto da virgem.
Veja também esta página:
Agrícola
é
considerado o
pai da geologia como ciência.
Cardano
(também grafado como Jerôme Cardan, Hieronymus
Cardanus, Dzhirolamo
Kardano, etc.) foi um médico, físico e
matemático italiano.Cardano foi o iniciador da teoria das equações algébricas.
Criou o sistema de transmissão com eixo cardã, utilizado até hoje em motocicletas e veículos 4×4.
Foi, também, o primeiro a descrever clinicamente a febre tifóide.
Cardano publicou (apropriando-se de) o método de Scipione del Ferro e Tartaglia p/ resolver a equação algébrica de 3º grau.
Em 1550, discutiu em seu livro De Subtilitate as diferenças entre forças elétricas e forças magnéticas.
Tycho
foi um nobre e astrônomo e alquimista dinamarquês.
Foi o astrônomo imperial de Rodolfo II, imperador do Sacro
Império Romano-Germânico, rei
da Boêmia e rei
da
Hungria.
Tycho foi o último dos grandes astônomos a praticar astronomia óptica, sem telescópio. Apesar disso, obteve dados precisos a 1/60 de grau. Seus resultados eram acurados, pois fazia a média de medições repetidas, procedimento inovador para a época. Forneceu dados astronômicos para Kepler.
Tycho foi um dos seus primeiros utilizadores dos logaritmos, inventados por Napier, que simplificaram os cálculos manuais, bem como da trigonometria esférica, como veremos na aula A Revolução na Matemática.
Em 1572, Tycho observou uma nova estrela na constelação de Cassiopéia, hoje conhecida como SN1572. Chamou-a de nova, cunhando o termo, usado até hoje.
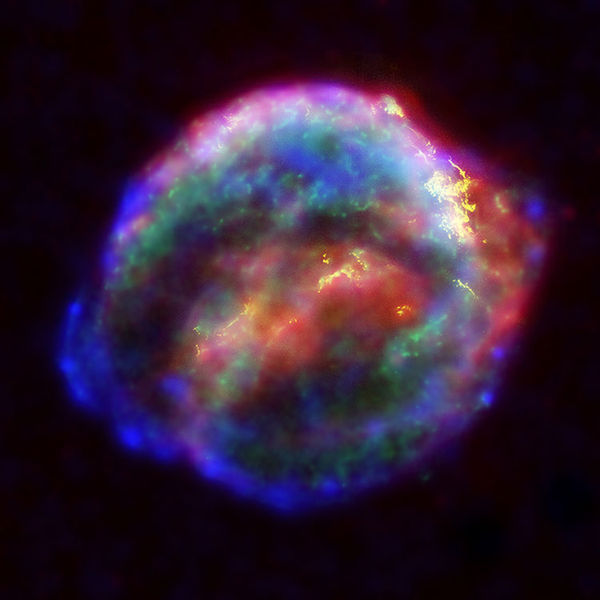
Da mesma forma, mostrou que os cometas não são meros fenômenos atmosféricos, como se pensava antes. Essa descoberta abalou a fé na doutrina cristã-aristotélica da perfeição e imutabilidade da esfera celeste. O céu muda!
No fim da vida, foi ajudado por Kepler (vide adiante), a quem, após muita insistência deste, legou seus dados sobre a órbita de Marte, ciumentamente guardados.
Em sua homenagem, há a cratera Tycho na Lua, a cratera Tycho Brahe em Marte e o Planetário Tycho Brahe, em Copenhague.
Kepler
foi matemático, astrônomo e astrólogo
alemão
luterano.Aos seis anos de idade, observou o Grande Cometa de 1577, o que despertou-lhe o amor à Astronomia que lhe acompanhou por toda a vida.
Como tantos filósofos naturais da sua época, fazia horóscopos para clientes ricos para sobreviver. Nessa época, não se separava a Astrologia da Astronomia.
Kepler considerava o Harmonices Mundi (A Harmonia do Mundo, 1619) seu maior trabalho, que foi, também, a primeira defesa publicada do sistema de Copérnico. Nele, relata suas descobertas sobre o conceito de congruência com relação a diversas categorias do domínio físico: regularidades em geometria tridimensional, as relações entre diferentes espécies de magnitude, os princípios da harmonia na música e da organização do Sistema Solar. Na última seção do livro, relata sua descoberta da então chamada Terceira Lei do movimento planetário.
Enquanto filósofos desde Pitágoras falavam da música das esferas, Kepler procurava harmonias físicas no movimento planetário. Por exemplo, a velocidade angular máxima da Terra medida a partir do Sol varia em um semitom (proporção de 16:15), de mi para fá, enquanto Venus varia muito pouco, 25:24.
Ele
descobriu que cada um dos
cinco sólidos
platônicos
poderiam ser unicamente
inscritos
e circunscritos por
órbitas esféricas;
encaixando estes
sólidos,
cada um envolto em
uma esfera, uma dentro da
outra, produziria
seis
camadas, correspondentes aos seis
planetas
conhecidos, Mercúrio,
Vênus, Terra, Marte,
Júpiter e
Saturno, que, dentro
dos limites de
precisão das observações
astronômicas, disponíveis
à época, aproximavam bem os
raios relativos das órbitas
de cada planeta,
assumindo que os planetas circulassem
o Sol.
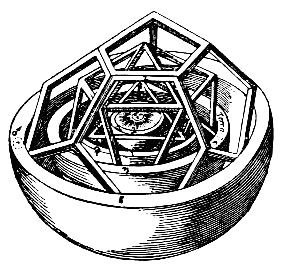
Kepler constatou que a maior discrepância ocorria na relação entre Marte e Júpiter, como se 'faltasse' um planeta nos cálculos de Kepler. Curiosamente, é nessa região que existe o cinturão de asteróides, o qual só foi descoberto em 1801.
Kepler também estudou Óptica e o olho humano.
De um ponto de vista na Terra, quando Marte se aproxima da oposição ao Sol, ele começa um período de movimento retrógrado, o que significa que vai parecer se mover para trás em um movimento de loopingcom relação às estrelas de fundo.
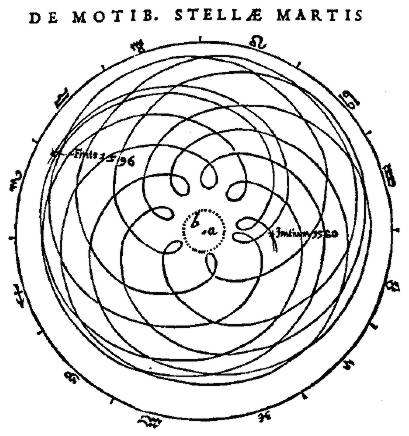
A duração deste movimento retrógrado dura cerca de 72 dias e Marte atinge o seu pico de luminosidade no meio deste movimento.
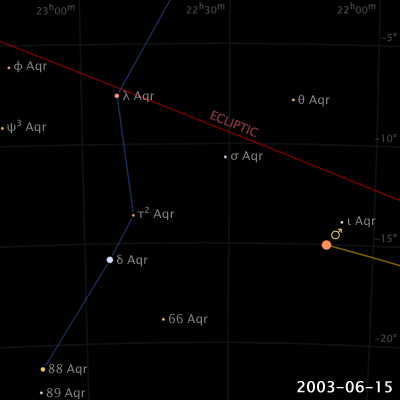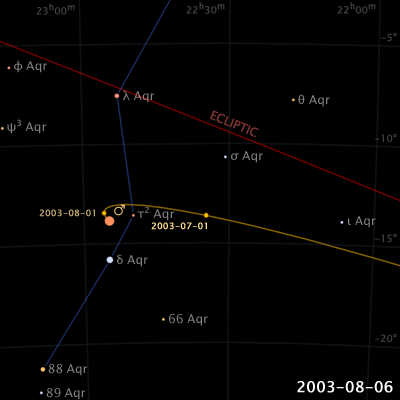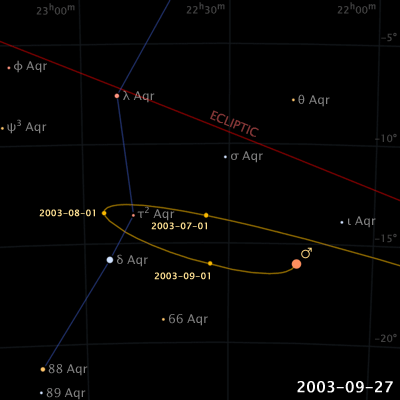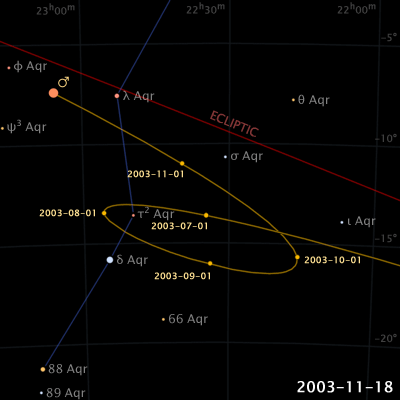fonte:
Wikipédia.
http://en.wikipedia.org/wiki/File:Apparent_retrograde_motion_of_Mars_in_2003.gif.
Para investigar esse problema, Kepler precisava muito dos precisos dados de Tycho Brahe que, só após muita insistência, legou seus dados ciumentamente guardados.
Inicialmente, Kepler tentou ajustar a órbita de Marte a uma círcunferência mas não conseguiu. Teve de abandonar as 'perfeitas' órbitas circulares e supor órbitas elípticas, as quais, finalmente, deram certo. E, sobre elas, afinal, conseguiu formular suas famosas três leis, publicadas em seu Astronomia Nova, de 1609.
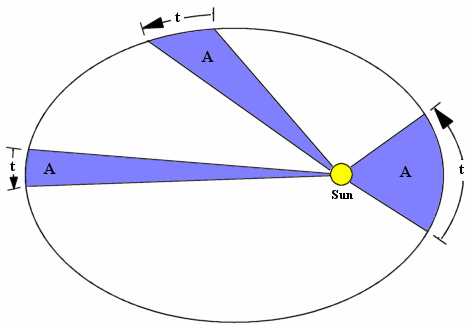
Kepler também estudou a teoria atômica e o efeito de ‘empacotamento’.
Em sua homenagem, há a cratera Kepler e o asteróide Kepler.
Continue
conhecendo
as contribuições
de Galileu e Newton para a Ciência.Voltar à Parte Anterior
Voltar a Minhas Aulas.
Voltar ao começo desta página
Voltar à página principal de Física Interessante
